Tema: Los sistemas de referencia y la ideología racionalista-matematicista

Un sistema de referencia es un punto o marco que se toma como base o fundamento para la realización de cálculos en torno a él. En este sentido puramente matemático, no constituye en sí ninguna representación de la realidad física, sino que solamente se utiliza a efectos puramente instrumentales o utilitarios.

Es por ello que siempre es posible realizar un cambio de sistema de coordenadas con el fin de realizar los cálculos de un modo más sencillo o rápido, sin que por ello mismo se suponga que el nuevo sistema de referencia en torno al cual se realicen los cálculos implique, igual que en el caso original, una genuina representación de la realidad física.

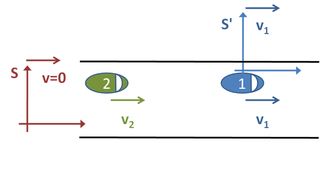
Pongamos un ejemplo. Tenemos dos coches que se mueven por una carretera. Estos dos coches se mueven a velocidades constantes y distintas si son observados desde un sistema de referencia "estacionario" S adjunto a la carretera.



En un momento determinado ambos coches aparecen separados por 100 metros de distancia el uno respecto al otro. El coche de delante (número 1, de color azul) viaja a una velocidad de 10 m/s, y el coche de detrás (número 2, de color verde) viaja a una velocidad de 20 m/s. Si queremos hallar en qué instante del tiempo alcanzará el segundo coche al primero, cabe poder elegir, para resolver el caso, tres "sistemas de referencia" distintos.

En primer lugar, podríamos observar los dos coches estando nosotros encima de la carretera. Definimos nuestro sistema de referencia S del siguiente modo: estamos quietos a un lado de la carretera y accionamos un cronómetro en el instante mismo en que pasa el segundo coche delante nuestro, lo cual ocurre justo cuando la distancia de separación entre los dos coches es de 100 metros. Como hemos dicho que los dos coches van a velocidades uniformes, podemos determinar sus posiciones con las siguientes fórmulas:

x₁ (t) = x₀ + v₁t ; En el instante t = 0, tenemos para el primer coche: x₁ (t) = 100 + 10t

x₂ (t) = x₀ + v₂t ; En el instante t = 0, tenemos para el segundo coche: x₂ (t) = 0 + 20t, x₂ (t) = 20t

Vemos que en el tiempo t = 0 las fórmulas nos indican que el primer coche está a 100 metros más allá de nosotros y el segundo coche está justo delante nuestro.

Hay que encontrar el tiempo en que x₁ = x₂. Por tanto igualamos ambas ecuaciones y tenemos:

100 + 10t = 20t;

100 = 10t;

t = 10 segundos.

A su vez, podemos escoger un sistema de referencia S´ situado en el primer coche. En este caso, el primer coche se considerará estacionario y el segundo coche se estará aproximando a una velocidad de v₂ - v₁ = 20 m/s - 10 m/s = 10 m/s. Para poder alcanzar al primer coche, el segundo necesitará de un tiempo igual a:

t = d / (v₂ - v₁) = (100 m) / (10 m/s) = 10 segundos.

Como se vé obtenemos el mismo resultado de antes. Y obsérvese también que esta segunda forma de resolver el problema ha sido más fácil.

El tercer sistema de referencia iría unido al segundo coche. Este caso es igual al anterior, sólo que aquí se considera estacionario al segundo coche mientras que al primero se le considera yendo hacia atrás a una velocidad de 10 m/s.

De esta forma vemos que podemos pasar a otro sistema de referencia los cálculos y medidas realizadas en base a un sistema de referencia previo o primeramente elegido, obteniendo en ambos los mismos resultados.

Ésa es la razón por la que los científicos consideran matemáticamente equivalentes los sistemas geocéntrico-heliocéntrico, porque da igual que, para la realización de los cálculos, se tome como sistema de referencia (es decir, que se considere en reposo) a la Tierra o al Sol para la realización de los cálculos.

Por ejemplo, Stephen Hawking admitía en su último libro publicado lo siguiente:


"Así pues, ¿qué sistema se ajusta más a la realidad, el ptolemaico o el copernicano? Aunque es bastante habitual que se diga que Copérnico demostró que Ptolomeo estaba equivocado, eso no es verdad. (…) podemos utilizar ambas visiones como modelo de Universo, ya que nuestras observaciones del firmamento pueden ser explicadas tanto si suponemos que la Tierra o el Sol están en reposo. A pesar de su papel en los debates filosóficos sobre la naturaleza de nuestro Universo, la ventaja real del sistema copernicano es simplemente que las ecuaciones de movimiento son mucho más simples en el sistema de referencia en que el Sol se halla en reposo."

Fuente: "El Gran Diseño". Stephen Hawking y Leonard Mldoninow. Ed. Crítica. Página 50.


Así pues vemos que la única razón por la que un científico pueda autodenominarse heliocentrista es por una pura razón de conveniencia, es decir, por razones puramente ideológicas. El problema, como muy bien decía el gran cosmólogo George Ellis, es que esto no lo reconocen (o no quieren reconocerlo) la mayoría de los cosmológos en sus afirmaciones. George Ellis dice lo siguiente:


"La gente debe ser consciente de que existe una gama de modelos que podrían explicar las observaciones, (...). Por ejemplo, yo podría contruirte un universo esféricamente simétrico con la Tierra en su centro, y tú no podrías refutarlo basándote en las observaciones. (...) Tú solamente podrías rechazarlo por razones filosóficas. En mi opinión no hay absolutamente nada de malo en ello. Lo que quiero sacar a la luz es el hecho de que estamos usando criterios filosóficos a la hora de elegir nuestros modelos. Muchos cosmólogos tratan de ocultar esto.”

Fuente: “Profile: George F. R. Ellis,” W. Wayt Gibbs, Scientific American, Octubre de 1995, Vol. 273, No. 4, p. 55.


El problema de todo esto, evidentemente, radica en la posibillidad fisica de los resultados que puedan derivarse de un cálculo matemático. Es obvio que, matemáticamente, podrá calcularse de manera igual el tiempo de aproximación mutua de una persona y de la Tierra, tanto si partimos de considerar que es el hombre el que se va acercando o bajando hacia la Tierra como si es la Tierra la que se va "acercando" o "subiendo" hacia el hombre; digo que matemáticamente el resultado del cálculo del tiempo de "colisión" (mediante las correspondientes ecuaciones) será el mismo partiendo de ambos sistemas, pero no es menos obvio que uno de esos sistemas tiene fundamento físico y el otro carece de él.

El hecho de que se pueda considerar ambos sistemas como igualmente viables, desde un punto de vista físico, constituye una invasión de carácter ilegítimo por parte de las matemáticas dentro del campo de la física y, por ende, de la filosofía (o de las implicaciones filosóficas dentro de la física y la cosmología).

Propiamente, el matematicismo es una forma de logicismo, es decir, un método encubierto en virtud del cual se trata de hacer creer en una determinada "metafísica" o "cosmovisión" partiendo de un apriorismo ideológico y tratándolo de "fundamentar" a través de una supuesta metodología "neutral", en virtud de la cual, por medio de una concatenación (más o menos compleja) de sucesivas deducciones lógicas y matemáticas, se llega a una conclusión matemática que sirve de fundamento para una afirmación física completamente gratuita (tan gratuita como el punto de partida apriorístico del que se inició y que contenía en germen la conclusión final).

Entiéndase que éste es el modo racionalista de pensar que se inició con el método científico moderno. No tiene nada que ver con el uso de las matemáticas para cuestiones de ingeniería o tecnología, que es algo que fue utilizado siempre en todas la civilizaciones desde la antigüedad en adelante. Etienne Gilson, en su libro La Unidad de la Experiencia Filosófica, hace esta importantísima distinción cuando entra a analizar el pensamiento racionalista moderno que se inicia en el siglo XVII ( de la mano de Descartes, Galileo, Newton, etc...). Gilson observa que una cosa era la aplicación de las matemáticas para cuestiones prácticas o de ingeniería (arquitectura, navegación, etc...) en donde impera la ley de la prueba-ensayo-error, y otra cosa muy distinta es aplicar las matemáticas para las cuestiones teóricas filosóficas, es decir, utilizar las matemáticas como un fin en sí mismas en virtud de las cuales puedan inferirse legítimas conclusiones filosóficas.

Éste último caso corresponde a una mentalidad racionalista que, en última instancia, es una mentalidad matematicista, que trae consigo las propiedades de las matemáticas tomadas en sí mismas, y las generaliza considerándolas como criterios del pensamiento. No deja de ser, en cierta forma, lógica la idea de la ausencia de causalidad que impera en toda la mentalidad racionalista. Vista la estructura de una ecuación, los matematicistas, generalizando las propiedades de la misma, llegan a la conclusión de que no se puede decir nunca de algo que éste sea realmente el efecto de una causa o la causa de un efecto. Se podrá hablar de una cierta correlación basada en la experiencia, pero el concepto de causalidad queda completamente desterrado. "Debemos" a David Hume el haber desarrollado la mentalidad matematicista hacia sus consecuencias últimas.

A continuación, eliminado el concepto de causalidad, lógicamente se sigue la eliminación del concepto de finalidad. Y de la eliminación de los principios de causalidad y finalidad, se llega finalmente con Hegel a la eliminación lógica y definitiva del principio de no contradicción, consagrándose así, de manera definitiva, el relativismo absoluto y el asesinato de toda metafísica, que están en la base del pensamiento modernista (tanto el moderno fuerte que le dio origen como el posmoderno débil de sus últimas consecuentes manifestaciones) caracterizado por el trío del historicismo-hermenéutica-existencialismo (que de manera excelente recogiera y explicara el Cardenal Siri en su imprescindible libro Getsemaní).

Entiéndase que una vez que se abre la puerta al binomio: "apriorismo como punto de partida–desarrollo lógico-matemático del apriorismo", se llega siempre a una conclusión totalmente arbitraria (contenida potencialmente en el apriorismo del que se parte). Se trata de pseudosoluciones que se explican por sí mismas. Que se autocontienen dentro de su propio sistema artificialmente construido. Es decir, se caracterizan por un razonamiento puramente circular (coherente con la mera existencia de una reciprocidad carente de todo nexo causal, el cual queda eliminado, como vimos antes) del que nunca se puede sacar una auténtica conclusión explicativa o descriptiva de la realidad física. Y, no sólo eso, sino que además su sistema es infinitamente flexible (como las matemáticas mismas de las que siempre parten) para obtener cualquier resultado que, en virtud de aquel apriorismo de partida, se quiera llegar.

Me atrevería a decir que es una especie de "magia negra" o "hipnotizadora" que, no por las matemáticas mismas que en sí no son malas, sino por un uso (o mejor dicho, abuso) torticero de las mismas se trata de hacer creer, gracias a ellas, cualquier cosa.

El colmo de esta tendencia iniciada en el siglo XVII llegó, en el campo de la física o filosofía cosmológica, a la Teoría de la Relatividad de Einstein, capaz toda ella, en virtud de su aparato esencialmente matemático, de asimilarse a cualquier "realidad física" que se pueda imaginar o elaborar con la imaginación.

No sólo se construían los modelos matemáticos en primer lugar, sino que luego se les trataba de dar una traducción en la realidad física. Es decir, no se trataba ya de considerar a las matemáticas como un auxiliar en la comprensión de la realidad, sino que se trataba de "ajustar" la realidad a esas matemáticas salidas del caldo de cabeza del matemático.

Pongamos un ejemplo típico de física: la caída de un objeto desde una altura. Pongamos que se lanza a una velocidad inicial de 50 m/s desde una altura de 100 metros. Se trata de calcular el tiempo que tardará en llegar al suelo. Consideramos la acelaración de la gravedad = 10 m/s² , para simplificar. Consideramos el suelo como punto de referencia.

La ecuación del movimiento es la siguiente:

x = x₀ + v₀t + 1/2gt²; sustituyendo los valores queda:

0 = 100 -50t -1/2 · 10 · t²; ajustando queda una ecuación de segundo grado:

5t² + 50t -100 = 0; de la cual se obtienen dos raices: x₁ = 1,7 segundos, y x₂ = -11,7 segundos.

Evidentemente de las dos soluciones sólo una tiene sentido físico: la primera. Es decir el objeto tardará 1,7 segundos en llegar al suelo. La otra solución no tiene sentido físico ninguno.

Es decir: una cosa es que ambas raíces satisfagan (como, de hecho, satisfacen) la ecuación matemática en cuestión. Pero otra cosa distinta es que sólo una de ellas tenga sentido físico o se ajuste a la realidad, mientras que la otra carezca por completo de sentido en la realidad física (no existe el tiempo físico negativo, es absurdo).

Pues bien. Todos los conceptos matemáticos de la geometría de Riemann, de las fómulas matemáticas de Fitzgerald-Lorenz, etc..., no eran en su origen más que "juegos" matemáticos, elaborados sin ningún sentido físico. Fue Einstein el que quiso darles un sentido físico (curvatura del espacio, contracción de la materia, dilatación del tiempo, etc...).

Y a su vez, llevó a sus últimas consecuencias el factor matemático de la invarianza de los sistemas de referencia, utilizando para ello el aparato matemático de Gregorio Ricci-Curbastro y su famoso cálculo tensorial que permitía la reciprocidad e intercambio de cualquier variable con otra (con independencia de las diferencias substanciales o físicas existentes entre ellas) para la obtención de cualquier resultado matemático, por muy disparatado que fuera en lo que a sus conclusiones o traducciones físicas se refiere.

De esta forma se daba "base" matemática al intercambio o amalgamiento de variables espaciales con variables temporales acuñándose el término de "espacio-tiempo", así como se inventaban nuevas realidades físicas por razones de exigirlas las apriorísticas ecuaciones matemáticas: así, si la ecuación daba como resultado infinito (∞), eso quería decir no que la ecuación matemática estuviera mal, sino que debía haber en la realidad física algo que se ajustara a lo predicho por la ecuación matemática.

Entiéndase el cambio de perspectiva completamente esquizofrénico de todo esto. Repito: con el método científico moderno ya no se trata de ajustar las matemáticas a la realidad (como podía hacer la autolimitada geometría realista de Euclides, por ejemplo) sino que se trata de que la realidad física se ajuste a las conclusiones matemáticas, a las que arbitrariamente se llega. Por ejemplo, la solución infinita antes mencionada se ajustaría (según Hawking) a la presunta existencia de un llamado "agujero negro". Lo mismo con todas las demás sustancias puestas ad hoc como consecuencia de las ecuaciones: inflación, materia oscura, energía oscura y cualquier cosa que se pueda imaginar.

Desde luego tenía razón George Ellis. Con las matemáticas se puede construir cualquier modelo cosmológico. El problema está en que los cosmólogos no quieren reconocer que se mueven por apriorismos ideológicos a la hora de elaborar sus complejas ecuaciones diseñadas para dar la solución que a ellos les plazca y luego concluir que eso se corresponde con la realidad física.

Nunca se insistirá lo suficiente en las terribles consecuencias e implicaciones FI-LO-SÓ-FI-CAS que supuso la eliminación de la Tierra como sistema de referencia fijo de todo el Universo. Una vez conseguido el "éxito" del nuevo método en la cosmología, no tardaría en ampliarse a todas las demás ramas de la filosofía (política, jurídica, moral, social, economía, psicología, etc...) para justificar, "por razones científicas" (mediante ese método "neutro"), cualquier cosa que se imaginara uno.